Double Star Calculator - Documentation

This document provides a detailed methodological description of the procedures implemented in the Double Star Calculator [1]. It is intended to serve as a technical reference for users of the Double Star Calculator. The current version of this document is located at [2].

The Double Star Calculator derives a comprehensive set of astrometric and kinematic quantities for double star systems, including angular and spatial separations, position angles, proper motion vectors, distance estimates, tangential and spatial velocities, and derived physical parameters such as absolute magnitudes, luminosities, and mass estimates. All computations are based on established geometrical relations, classical error propagation, and standard astronomical conventions. The mathematical formulations underlying each calculation are documented to ensure transparency, reproducibility, and independent verification of the results.

Core Astrometric and Kinematic Functions

This section describes the core astrometric and kinematic computations performed for stars and double star systems. These calculations form the basis of the physical interpretation and are directly used in the analyses.

Angular Separation

This section describes the mathematical formulation used to compute the angular separation (ρ) between two stellar components (A and B) based on Gaia astrometric data.

Arguments

Results

Angular Separation

To calculate the angular separation ρ between two celestial objects based on their Gaia DR3 equatorial coordinates (α_A, δ_A) and (α_B, δ_B), the Haversine Formula is used. This method is numerically superior to the Spherical Law of Cosines for small angular distances, as it avoids precision loss when the cosine of a small angle approaches. The calculation is performed in radians using the following steps:

Δδ = δ_{B} - δ_{A}

Δα = α_{B} - α_{A}

hav ((ρ)) = \sin^{2} (\frac{Δ δ}{2}) + \cos (δ_{A}) \cdot \cos (δ_{B}) \cdot \sin^{2} (\frac{Δ α}{2})

Calculation of Separation ρ :

The final angular separation is derived using the atan2(y, x) function. The atan2 implementation is preferred because it is better conditioned for all angles and avoids potential domain errors due to floating-point rounding.

ρ = 2 \cdot atan2 (\sqrt{hav(ρ)}, \sqrt{1 - hav(ρ)})

Error Propagation

The uncertainty of the separation was derived using first-order Gaussian error propagation, assuming uncorrelated uncertainties in right ascension and declination:

σ_{ρ} = \sqrt{\sum_{i=1}^{4} {(\frac{\partial ρ}{\partial x_{i}} \cdot σ_{x_{i}})}^{2}}

Where x_i ∈ {α_A, δ_A, α_B, δ_B}

Position Angle

This function computes the position angle θ of a double star measured from North towards East (0°–360°), based on Gaia DR3 coordinates of the two components.

Arguments

Right ascension: α_A, α_B
Declination: δ_A, δ_B
Astrometric uncertainties: σ_{α_A}, σ_{δ_A}, σ_{α_B}, σ_{δ_B}

Results

θ: position angle from North → East → South → West (degrees, 0°–360°)
σ_θ: uncertainty of the position angle (degrees)

Position Angle

The position angle θ is calculated using the arctangent of the differential coordinates, where atan2(y, x) denotes the quadrant-correct two-argument arctangent, ensuring the correct quadrant of the position angle.

θ = atan2 (\cos δ_{B} \cdot \sin (α_{B} - α_{A}), \cos δ_{A} \cdot \sin δ_{B} - \sin δ_{A} \cdot \cos δ_{B} \cdot \cos (α_{B} - α_{A}))

The resulting angle is converted to degrees and shifted to the range 0°–360°.

Error Propagation

The uncertainty σ_θ is calculated using first-order Gaussian error propagation, based on the partial derivatives of atan2:

σ_{θ} = \sqrt{\sum_{i=1}^{4} {(\frac{\partial θ}{\partial x_{i}} \cdot σ_{x_{i}})}^{2}}

Where x_i ∈ {α_A, δ_A, α_B, δ_B}

Separation and position angle as a function of Epoch

The Double Star Calculator extrapolates the position of two stars, as well as their separation and position angle, from the Gaia DR3 reference epoch J2016.0 to user-defined target epochs (Δt = target-epoch - J2016.0). The calculation assumes a linear motion model over time.

Coordinates are projected using a linear motion model. The calculation accounts for the spherical geometry of the celestial coordinate system. The total uncertainty is calculated using Gaussian error propagation, combining the initial position error with the cumulative error of the proper motion over the elapsed time.

Right Ascension for target epoch

α_{target-epoch} = α_{ref} + (\frac{μ_{α *}}{\cos (δ_{ref})}) \cdot Δt

Declination for target epoch

δ_{target-epoch} = δ_{ref} + μ_{δ} \cdot Δt

Error Propagation

The total uncertainty at the target epoch is calculated using Gaussian error propagation.

σ_{α, total} = \sqrt{σ_{α, ref}^{2} + {(\frac{Δt \cdot σ_{μ_{α *}}}{\cos (δ_{ref})})}^{2}}

σ_{δ, total} = \sqrt{σ_{δ, ref}^{2} + {(Δt \cdot σ_{μ_{δ}})}^{2}}

Parameters

α_ref : Right Ascension at reference epoch J2016.0
δ_ref : Declination at reference epoch J2016.0
μ_α* : Proper motion in Right Ascension (μ_α ⋅ cos(δ) (mas/year))
μ_δ : Proper motion in Declination (mas/year)
σ_α : Standard uncertainty of the Right Ascension
σ_δ : Standard uncertainty of the Declination

Spatial Separation

This function calculates the spatial separation between two stars in parsecs, using their distances and angular separation. It also computes the uncertainty of the spatial separation via error propagation.

Arguments

d_A : Distance of star A
d_B : Distance of star B
θ : Angular separation in radians

Results

s – spatial separation in parsecs
σ_s – uncertainty of spatial separation

Spatial separation

s = \sqrt{{d_{A}}^{2} + {d_{B}}^{2} - 2 \cdot d_{A} \cdot d_{B} \cdot \cos (θ)}

Error propagation

The uncertainty of the spatial separation is calculated using partial derivatives:

σ_{s} = \sqrt{{(\frac{∂s}{{∂d}_{A}} \cdot σ d_{A})}^{2} + {(\frac{∂s}{{∂d}_{B}} \cdot σ d_{B})}^{2} + {(\frac{∂s}{∂θ} \cdot σ θ_{rad})}^{2}}

Note: The linear error propagation assumes that the relative parallax uncertainties are small. Larger relative uncertainties are approximated using first-order Gaussian propagation due to the non-linear transformation from parallax to distance.

Parallax Significance Indicator

This indicator quantifies whether the observed difference in parallaxes between two stars is statistically significant or merely a result of measurement uncertainties.

A high significance indicates that the stars are physically located at different distances, whereas a low significance suggests that the stars could be at the same distance within their measurement errors. The indicator is calculated by dividing the absolute difference of the parallaxes by the combined standard deviation:

S_{ϖ} = \frac{| ϖ_{A} - ϖ_{B} |}{\sqrt{σ_{ϖ, A}^{2} + σ_{ϖ, B}^{2}}}

Classification Thresholds:

The Parallax Significance Indicator is mapped to qualitative labels to simplify the interpretation of the 3D data:

Parallax Significance	Label	Status	Description
0 ≤ σ < 3	LOW	Stat. unresolved	The parallax difference is within the 3-sigma measurement uncertainty; 3D separation is statistically unresolved.
3 ≤ σ < 5	MED	Moderate	Difference is likely real, but the 3D distance carries significant uncertainty.
σ ≥ 5	HIGH	Significant	Highly significant difference. Stars are clearly located at different depths.

Example:

Spatial Separation                 :       38.97     pc
  1-Sigma Range                    : [     36.55,    41.39] pc
  Significance                     :       13.09     σ 
  Note: High-confidence 3D separation

3D Space Velocity Vector Angle Analysis

Evaluating whether a star pair shares a common space motion (co-moving pair) or merely represents a chance alignment requires comparing their three-dimensional space velocity vectors ${\vec{v}}_{1}$ and ${\vec{v}}_{2}$ . The angle $θ$ between these two 3D vectors provides a direct indicator of velocity alignment in space.

3D Space Velocity Vector Construction

For each component, the tangential velocity components derived from proper motions ( $μ_{α} *$ and $μ_{δ}$ in mas/yr) and distance ( $d$ in parsecs) are converted into physical velocities (km/s) using the astronomical conversion factor $k = 4.74057$ $km·yr/(pc·s·mas)$ :

\vec{v} = [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}] = [\begin{matrix} k \cdot (\frac{μ_{α} *}{1000}) \cdot d \\ k \cdot (\frac{μ_{δ}}{1000}) \cdot d \\ v_{r} \end{matrix}]

where $μ_{α} * = μ_{α} cos δ$ is the true right ascension proper motion and $v_{r}$ is the line-of-sight radial velocity in km/s.

Numerically Stable 3D Vector Angle

The opening angle $θ$ is computed using the $atan2$ of the cross-product magnitude and dot product:

θ = atan2 (∥ {\vec{v}}_{1} \times {\vec{v}}_{2} ∥, {\vec{v}}_{1} \cdot {\vec{v}}_{2}) \cdot (\frac{180^{ˆ}}{π})

where the vector cross-product magnitude $∥ {\vec{v}}_{1} \times {\vec{v}}_{2} ∥$ and dot product ${\vec{v}}_{1} \cdot {\vec{v}}_{2}$ are defined as:

∥ {\vec{v}}_{1} \times {\vec{v}}_{2} ∥ = \sqrt{{(v_{1, y} v_{2, z} - v_{1, z} v_{2, y})}^{2} + {(v_{1, z} v_{2, x} - v_{1, x} v_{2, z})}^{2} + {(v_{1, x} v_{2, y} - v_{1, y} v_{2, x})}^{2}}

{\vec{v}}_{1} \cdot {\vec{v}}_{2} = v_{1, x} v_{2, x} + v_{1, y} v_{2, y} + v_{1, z} v_{2, z}

Uncertainty Propagation via Numerical Finite Differences

The calculation depends on 8 observational parameters $\vec{x} = (μ_{α, 1}, μ_{δ, 1}, d_{1}, v_{r, 1}, μ_{α, 2}, μ_{δ, 2}, d_{2}, v_{r, 2})$ with associated standard errors $σ_{i}$ . Assuming uncorrelated errors, total uncertainty $σ_{θ}$ is propagated according to Gaussian error propagation:

σ_{θ} = \sqrt{\sum_{i = 1}^{8} {(\frac{\partial θ}{\partial x_{i}} \cdot σ_{i})}^{2}}

The partial derivatives $\frac{\partial θ}{\partial x_{i}}$ are computed numerically using 2nd-order central finite differences with an adaptive step size $h_{i}$ :

\frac{\partial θ}{\partial x_{i}} \approx \frac{θ (x_{i} + h_{i}) - θ (x_{i} - h_{i})}{2 h_{i}} mo> where h_{i} = max (| x_{i} | \cdot 10^{-6}, 10^{-8})

This scale-invariant step size prevents numerical truncation errors for both very large parameters (e.g. distances) and small values (e.g. low proper motions).

Proper Motion and Velocity Analysis

This function performs a kinematic analysis of a single star based on Gaia astrometric data. It derives the direction and magnitude of the proper motion vector, the tangential velocity, and, if available, the total space velocity including the radial component. All quantities are accompanied by uncertainty estimates.

Proper Motion Vector Angle

The position angle of the proper motion vector is calculated relative to the north direction, measured counterclockwise from north through east (0°–360°). The quadrant-correct two-argument arctangent is used.

θ = atan2 (μ_{α *}, μ_{δ})

Here, μ_α* and μ_δ denote the proper motion components in right ascension and declination, respectively.

Uncertainty of the Proper Motion Angle

The uncertainty of the proper motion position angle (σ_θ) is derived via Gaussian error propagation of the atan2 function. By using partial derivatives with respect to μ_α* and μ_δ, the following equation provides an error estimation that accounts for the relative magnitudes of the proper motion components:

σ_{θ} = \sqrt{{(\frac{μ_{δ}}{μ_{α *}^{2} + μ_{δ}^{2}} σ_{μ_{α *}})}^{2} + {(\frac{- μ_{α *}}{μ_{α *}^{2} + μ_{δ}^{2}} σ_{μ_{δ}})}^{2}}

Total Proper Motion

The total proper motion is calculated as the magnitude of the proper motion vector:

μ = \sqrt{μ_{α *}^{2} + μ_{δ}^{2}}

Uncertainty of Total Proper Motion

σ_{μ} = \sqrt{{(\frac{μ_{α *}}{μ} \cdot σ_{μ_{α *}})}^{2} + {(\frac{μ_{δ}}{μ} \cdot σ_{μ_{δ}})}^{2}}

Tangential Velocity

The tangential velocity is derived from the total proper motion and the parallax:

V_{t} = 4.74057 \cdot \frac{μ}{ϖ}

The numerical factor 4.74057 converts proper motion in milliarcseconds per year and distance in parsecs into velocity in km s⁻¹.

Uncertainty of Tangential Velocity

σ_{V_{t}} = \sqrt{{(\frac{4.74057}{ϖ} \cdot σ_{μ})}^{2} + {(\frac{4.74057}{ϖ^{2}} \cdot μ \cdot σ_{ϖ})}^{2}}

Space Velocity

This equation calculates the 3D velocity magnitude of a single star by combining its tangential and radial velocity components. For details refer to chapter Relative Velocity (3D) Difference.

By default, the Radial Velocity is retrieved from the Gaia DR3 record. If this data is missing, the Double Star Calculator automatically queries the SIMBAD database as a fallback. In this case, the field is labeled Radial Velocity (Simbad) and includes the corresponding Bibcode to identify the original scientific publication and its precision. If a Radial Velocity measurement is available, the total space velocity is computed as:

V = \sqrt{{V_{t}}^{2} + {V_{r}}^{2}}

Uncertainty of Space Velocity

σ_{V} = \sqrt{{(\frac{V_{t}}{V} \cdot σ_{V_{t}})}^{2} + {(\frac{V_{r}}{V} \cdot σ_{V_{r}})}^{2}}

Results

Proper motion angle and uncertainty (degrees)
Total proper motion and uncertainty of total proper motion (mas/yr)
Tangential velocity and uncertainty of tangential velocity (km/s)
Total space velocity and uncertainty of total space velocity (km/s)

Kinematic and Dynamical Linkage Analysis

This chapter describes algorithms to analyze the association between the two components of a double star. It details the calculation of the traditional Harshaw rPM (2D) algorithm and evaluates potential associations based on the Uncertainty Weighted Likelihood Estimator (UWLE). Furthermore, the equations describing orbital and binding dynamics are presented.

Harshaw 2D Methodology (rPM)

The Harshaw method [3] focuses on the ratio of Proper Motion (rPM), a dimensionless quantity comparing the angular velocity difference to the maximum magnitude. It is robust against distance uncertainties but ignores depth (parallax) and radial motion.

Proper motion in Right Ascension: $μ_{α * A}$ , $μ_{α * B}$
Proper motion in Declination: $μ_{δ A}$ , $μ_{δ B}$

μ_{A} = \sqrt{μ_{α * A}^{2} + μ_{δ A}^{2}} μ_{B} = \sqrt{μ_{α * B}^{2} + μ_{δ B}^{2}}

The dimensionless ratio of proper motion (rPM) is then computed using consistent tracking of the components:

rPM = \frac{\sqrt{{(μ_{α * A} - μ_{α * B})}^{2} + {(μ_{δ A} - μ_{δ B})}^{2}}}{max (μ_{A}, μ_{B})}

Harshaw Classification Levels

Indicator Type	Threshold	Classification
Harshaw rPM	< 0.2	CPM (Common Proper Motion)
Harshaw rPM	0.2 - 0.6	SPM (Similar Proper Motion)
Harshaw rPM	> 0.6	DPM (Distinct Proper Motion)

Uncertainty-Weighted Likelihood Estimator

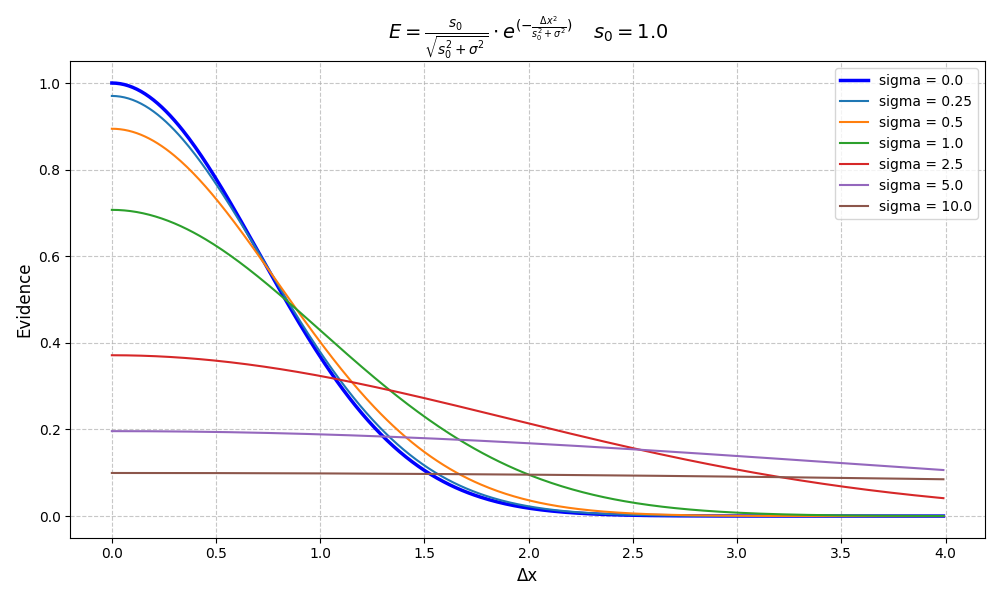
The core algorithm uses a variance-summation model. The Evidence Indicator E is defined by a Gaussian kernel multiplied by a normalization pre-factor that accounts for the relative weight of the measurement uncertainty.

E = \frac{s_{0}}{\sqrt{{s_{0}}^{2} + σ^{2}}} \cdot e^{(- \frac{Δ x^{2}}{s_{0}^{2} + σ^{2}})}

E - (Evidence Indicator): The final probability score normalized between 0.0 to 1.0
Δx - (Difference Magnitude): The magnitude of the difference between the observed properties of Star A and Star B
σ - (Combined Uncertainty): The propagated measurement error of the uncertainty of the difference Δx
s₀ - (Scale Parameter): A constant defining the sensitivity or the "characteristic width" of the estimator

Normalization Pre-factor: This term term of the equation above acts as a data-quality weight. It has two functions:

Data Quality Weighting: If the measurement uncertainty σ is large compared to the scale parameter s₀, the maximum achievable evidence is automatically attenuated, reflecting the low reliability of the underlying data and to account for the reduced statistical confidence.
Convergence: In the idealized case of perfectly precise measurements (σ → 0), the pre-factor becomes 1. In this state, the estimator behaves like a standard Gaussian distribution where a difference of zero results in a maximum evidence score of 1.0.

Impact of Measurement Uncertainty (σ)

This plot demonstrates how the Likelihood Estimator adapts to varying levels of data quality while keeping the scale factor constant (s₀ = 1.0).

Evidence Factor for different sigma — Likelihood Estimator for different σ and for a Scale Parameters s₀ = 1.0

Ideal Data (σ = 0): The reference curve (blue) appears in this case, the prefactor is calculated to 1.When measurements are perfectly precise, the evidence is solely determined by the observed difference Δx, reaching a maximum of 1.0 at zero difference.
Moderate Uncertainty (σ = 2.5 to 5): As uncertainty increases, the maximum possible evidence is attenuated. Even if Δx is zero, the score is reduced to reflect that the matching values might be coincidental due to the large error bars.
Low Reliability (σ = 10): In cases where the uncertainty is significantly larger than the scale factor s₀, the curve becomes very flat and the peak is heavily suppressed. This prevents the system from over-reporting high-confidence associations when the underlying data is noisy.

Note: An increasing σ not only lowers the peak (Data Quality Weighting) but also broadens the distribution, meaning that at high uncertainty levels, the estimator becomes less sensitive to small changes in Δx.

Velocity Evidence Indicator

A specialized version of the Uncertainty-Weighted Likelihood Estimator is used to calculate the Velocity Evidence Indicator. It evaluates the kinematic consistency of a pair by analyzing relative velocities while accounting for physical constraints and data quality.

1. Robustness against Signal-to-Noise (SNR) Issues

To maintain reliability in the presence of measurement noise, the algorithm monitors the Signal-to-Noise Ratio (SNR). In cases of a Low SNR (< 3.0), the system additionally calculates the Evidence Indicator based on the projected separation. This mitigates the risk of large radial distance uncertainties distorting the kinematic assessment.

2. Scale Factor Configuration (v₀)

The scale factor v₀ determines the tolerance of the likelihood curve. The algorithm distinguishes between two search modes:

Co-Moving (CoMov): Uses a fixed v₀ = 5.0 km/s. This provides a balanced filter suitable for identifying wide stellar associations and moving groups.
Potential Binary Systems (DS): Employs a dynamic v₀ based on gravitational scaling (v₀ ∝ √1/d). It is anchored to the El-Badry & Rix (2021) benchmark of 2.1 km/s at 1000 au. Closer pairs require a tighter velocity match, approximating the physical escape velocity limits.

3. Evidence Classification Labels

To assist in the interpretation of the numerical results (ranging from 0.0 to 1.0), the Velocity Evidence Index is categorized into four qualitative labels:

Evidence Index	Label	Interpretation
0.7 – 1.0	Strong	High probability of physical association (CoMov or Binary).
0.3 – 0.7	Moderate	Potential association; data supports kinematic similarity.
0.1 – 0.3	Weak	Low kinematic agreement; likely a chance alignment.
< 0.1	Unlikely	Significant velocity discrepancy; association improbable.

Distance Evidence Indicator

The Distance Evidence Indicator utilizes a specialized version of the Uncertainty-Weighted Likelihood Estimator to evaluate the spatial proximity of a stellar pair. By analyzing geometrical consistency and relative distance while accounting for physical constraints and data quality, it provides a robust measure of whether two stars are truly co-located.

1. Robustness against Signal-to-Noise (SNR) Issues

2. Scale Factor Configuration (s₀)

Depending on the selected analysis mode, the algorithm adjusts its internal scale factor (s₀) and units to match the expected physical dimensions:

Co-Moving Pairs (COMOV): Operates in Parsecs (pc) with s₀ = 1.0 pc. This scale is roughly equivalent to the Jacobi Radius of typical stellar clusters in the solar neighborhood, making it ideal for identifying wide associations

Binary Systems (WBS/TBS): Switches to Astronomical Units (au). The algorithm distinguishes between:

Wide Binaries (WBS): s₀ = 20,000 au, based on the statistical limits for wide pairs (Tian et al. 2020 [4]; El-Badry et al. 2021 [5])

Tight Binaries (TBS): s₀ = 1,000 au, focusing on dynamically stable systems as defined by Correa-Otto & Gil-Hutton (2017) [6]

3. Evidence Classification Labels

Similar to the kinematic assessment, the Distance Evidence Index is mapped to qualitative labels to provide a quick interpretation of spatial consistency:

Evidence Index	Label	Interpretation
0.7 – 1.0	Strong	Excellent spatial agreement; the pair is clearly co-located.
0.3 – 0.7	Moderate	Good spatial agreement; consistent with a common origin or group.
0.1 – 0.3	Weak	Marginal spatial agreement; distance difference is significant.
< 0.1	Unlikely	Significant spatial discrepancy; co-location is improbable.

Total Evidence Indicator

The kinematic and spatial results are synthesized into a single, unified metric. This provides a final assessment of the physical association between two stars. The total evidence is calculated using the geometric mean of the Velocity Evidence (E_velocity) and the Distance Evidence (E_distance):

E_{total} = \sqrt{E_{velocity} \cdot E_{distance}}

1. Final Probability Classification

The resulting index serves as the final "Confidence Score" for the pair's Co-Moving (CoMov) or Binary status:

Total Evidence	Final Label	Physical Interpretation
0.7 – 1.0	Strong	High confidence pair; kinematic and spatial data are fully consistent.
0.3 – 0.7	Moderate	Likely association; supported by data but may have moderate uncertainties.
0.1 – 0.3	Weak	Suspicious pair; discrepancies in either motion or distance suggest a chance alignment.
< 0.1	Unlikely	No physical association; the stars are very likely independent field stars.

Evidence Indicators - Summary

The table below provides a quick overview of the calculated UWLE Evidence Indicators and their parametrization:

Condition	Mode	Type	Distance Scaling s₀	Velocity Scaling v₀	Δx	Uncertainty
-	Co-Moving	COMOV	1.0 pc	5 km/s	spatial	σ_spatial
-	Wide Binaries (3D)	WBS	20,000 au	$\propto \sqrt{1 / d_{spatial}}$	spatial	σ_spatial
S_ϖ < 3.0	Wide Binaries (2D)	WBS	20,000 au	$\propto \sqrt{1 / d_{projected}}$	projected	σ_spatial
S_ϖ < 3.0	Tight Binaries (2D)	TBS	1,000 au	$\propto \sqrt{1 / d_{projected}}$	projected	σ_projected

3D Spatial Distance Probability Analysis

Determining the true 3D spatial separation ( $d_{3D}$ ) between two binary components from astrometric observations (such as Gaia parallaxes) involves significant measurement uncertainties. While the calculated 3D distance is typically represented as a mean value $μ$ with a standard deviation $σ$ , assessing whether the pair is consistent with a physically bound system benefits from a probabilistic treatment of the spatial separation uncertainty.

Physical Boundary Condition & Truncation Motivation

In observational astronomy, the projected separation on the sky plane ( $d_{proj}$ ) represents an absolute physical lower bound for the true spatial distance:

d_{3D} = \sqrt{d_{proj}^{2} + Δ z^{2}} \geq d_{proj}

where $Δ z$ is the unknown distance along the line of sight. Standard Gaussian models assign non-zero probabilities to values below $d_{proj}$ and even to unphysical negative distances. To eliminate these physical impossibilities, the probability density function is truncated below $d_{proj}$ and renormalized over the physically allowed domain $[d_{proj}, \infty)$ .

Cumulative Probability

Let the unconstrained 3D spatial separation be modeled as a normally distributed random variable $D \sim N (μ, σ)$ , where $μ = d_{3D}$ and $σ = σ_{3D}$ . The standard Gaussian cumulative distribution function $Φ (z)$ is given by:

Φ (z) = \frac{1}{2} [1 + erf (\frac{z}{\sqrt{2}})] mo> with z = \frac{x - μ}{σ}

To ensure numerical stability in the extreme upper tails of the distribution, the survival function $S (x) = P (D > x)$ is calculated via standard normal symmetry as $S (x) = Φ (- z)$ . The probability that the true distance lies above the physical lower bound $d_{proj}$ serves as the normalization factor $S (d_{proj})$ .

For any distance threshold $T > d_{proj}$ , the cumulative probability conditioned on $D \geq d_{proj}$ is derived as:

P (D \leq T ∣ D \geq d_{proj}) = \frac{P (d_{proj} \leq D \leq T)}{P (D \geq d_{proj})} = \frac{S (d_{proj}) - S (T)}{S (d_{proj})}

Dynamic & Astrophysical Threshold Evaluation

The probability pipeline evaluates the system against both dynamic thresholds specific to the pair's geometry and established astrophysical milestones:

Dynamic Relative Bound ( $2.0 \times d_{proj}$ ): Evaluates the immediate spatial neighborhood around the projected lower bound. This accounts for inclination effects along the sightline while providing an intuitive non-zero probability baseline
1,000 AU: Upper boundary for dynamically stable close binary systems (Correa-Otto & Gil-Hutton 2017)
2,500 AU & 10,000 AU: Benchmarks for classic wide binary regimes
20,000 AU: Galactic wide binary boundary (Tian et al. 2020; El-Badry et al. 2021)
206,265 AU (~1 pc): Galactic tidal limit / Jacobi radius in the solar neighborhood

Fixed thresholds that fall below the dynamic lower limits are automatically filtered out to ensure monotonically increasing evaluations.

Critical Binding Distance according to Letchford et al. (2022)

To physically assess whether a binary star system is gravitationally bound, the Double Star Calculator utilizes the specific binding energy approach defined by Letchford et al. (2022) [11]. A binary pair is considered gravitationally bound if the total energy of the system in the center-of-mass frame is negative.

The calculated threshold $D_{critical}$ serves as a physical upper integration limit within the lower-truncated normal distribution (3D Spatial Distance Probability Analysis). If the true 3D spatial separation exceeds $D_{critical}$ , gravitational attraction is insufficient to maintain a bound orbit against the observed relative velocity. Evaluating the cumulative probability distribution from the projected separation up to $D_{critical}$ directly yields the physical binding probability of the binary system.

E_{binding} = E_{kin} + E_{pot} < 0

By applying the reduced mass $μ = \frac{m_{A} \cdot m_{B}}{m_{A} + m_{B}}$ for the relative motion of two bodies, the energy balance is formulated as follows:

\frac{1}{2} \cdot μ \cdot {(Δ v_{3D})}^{2} - \frac{G \cdot m_{A} \cdot m_{B}}{D} < 0

Substituting and simplifying the reduced mass $μ$ , the condition for gravitational binding reduces to:

\frac{1}{2} \cdot {(Δ v_{3D})}^{2} < \frac{G \cdot (m_{A} + m_{B})}{D}

The critical binding distance $D_{critical}$ defines the exact spatial separation at which the kinetic energy of relative motion equals the gravitational potential energy ( $E_{binding} = 0$ ).

D_{critical} = \frac{2 \cdot G \cdot (m_{A} + m_{B})}{{(Δ v_{3D})}^{2}}

$D_{critical}$ : Critical spatial distance
$G$ : Newtonian constant of gravitation
$m_{A}, m_{B}$ : Masses of the primary and secondary components
$Δ v_{3D}$ : Magnitude of the 3D relative velocity difference between components

Integration into the Probability Framework

The threshold $D_{crit}$ serves as a physical upper integration limit within the lower-truncated normal distribution. If the true 3D spatial separation exceeds $D_{crit}$ , gravitational attraction is insufficient to maintain a bound orbit against the observed relative velocity. Evaluating the cumulative probability distribution from the projected separation $d_{proj}$ up to $D_{crit}$ directly yields the physical binding probability $P_{bound}$ of the binary system.

Orbital & Binding Dynamics

When a potential binary is identified, the tool evaluates the gravitational relationship:

Est. Orbital Period

The estimated time (in years) required for one full revolution. This calculation assumes the current projected separation as the semi-major axis of a circular orbit.

Escape Velocity (v_esc)

The maximum relative velocity at which the two stars remain gravitationally bound. If the measured velocity difference exceeds this threshold, the stars are considered "Likely Unbound."

Circular Orbital Velocity (v_circ)

The theoretical velocity required for a stable, perfectly circular orbit at the given separation. It serves as a benchmark for the "depth" of the gravitational bond.

Binding Indicator (η)

A dimensionless index representing the ratio of kinetic energy to the magnitude of gravitational potential energy.

η < 0.5	: Strongly bound system (deep gravity well)
0.5 ≤ η < 1.0	: Bound, but on a high-energy or highly eccentric orbit
η ≥ 1.0	: Unbound; the system has reached or exceeded escape velocity

Calculation of Orbital Period (P):

P_{} = \sqrt{\frac{r^{3}}{M_{A} + M_{B}}}

Calcuation of Escape Velocity (v_esc):

v_{esc} = 42.12 \cdot \sqrt{\frac{M_{A} + M_{B}}{r}}

Calcuation of Circular Orbital Velocity (v_circ):

v_{circ} = \frac{v_{esc}}{\sqrt{2}}

Calculation of the Binding Indicator (η):

η = {(\frac{v_{rel}}{v_{esc}})}^{2}

Derivation of the Binding Indicator (η)

Definition of specific energy:

ε = ε_{kin} + ε_{pot} = \frac{v_{rel}^{2}}{2} - \frac{G M}{r}

Definition of Escape Velocity:

\frac{v_{esc}^{2}}{2} = \frac{G M}{r}

Substitution:

ε = \frac{v_{rel}^{2}}{2} - \frac{v_{esc}^{2}}{2}

Final equation:

η = \frac{v_{rel}^{2} / 2}{v_{esc}^{2} / 2} = {(\frac{v_{rel}}{v_{esc}})}^{2}

Definitions:

r : Projected separation between the stars (in au)
M_A, M_B : Estimated masses of the individual stars (in solar masses, M_⊙)
P : Estimated orbital period (in years)
v_rel : Relative velocity (in km/s)
v_esc : Escape velocity (in km/s)
v_circ : Circular orbital velocity (in km/s)

Metallicity Analysis [M/H]

The Metallicity Analysis [M/H] routine is designed for the comparative analysis of the chemical composition of stellar pairs using Gaia DR3 GSP-Phot (Aeneas) data. By comparing the iron abundance ([M/H]), the algorithm assesses whether a stellar pair exhibits a consistent chemical signature—a primary indicator of a shared origin (co-natal stars). The methodology incorporates the statistical processing of asymmetric MCMC (Markov Chain Monte Carlo) confidence intervals, the calculation of combined uncertainties in quadrature, and a quality weighting based on photometric transit integrity.

1. Deriving Standard Deviation from MCMC Percentiles

Gaia GSP-Phot provides metallicity as the median of an MCMC sample, along with the 16th (lower) and 84th (upper) percentiles. To convert these asymmetric confidence intervals into a symmetric standard deviation $σ$ suitable for error propagation, the routine calculates the arithmetic mean of the absolute deviations:

σ_{M/H} = \frac{| [M/H] - {[M/H]}_{lower} | + | [M/H] - {[M/H]}_{upper} |}{2}

2. Statistical Significance (Z-Score)

To evaluate the chemical consistency between both stars, a Z-Score is calculated. While measurement errors are assumed to be independent and normally distributed, the statistical uncertainties from Gaia DR3 often underestimate systematic effects like parameter degeneracies. To ensure a robust comparison, a systematic uncertainty floor (σ_sys = 0.21 dex) is incorporated into the Gaussian error propagation. This floor is based on the Median Absolute Deviation (MedAD) observed in validation studies (cf. R.Andrae, M.Fouesneau et al. (2023) [7]), comparing Gaia GSP-Phot with high-resolution spectroscopy.

σ_{combined} = \sqrt{σ_{A}^{2} + σ_{B}^{2} + σ_{sys}^{2}}

The resulting Z-Score represents the number of standard deviations separating the two measurements:

Z = \frac{| {[M/H]}_{A} - {[M/H]}_{B} |}{σ_{combined}}

3. Photometric Metallicity Confidence Factor (PMCF)

To evaluate the reliability of the spectroscopic data, a proprietary Photometric Metallicity Confidence Factor (PMCF) is calculated. This factor accounts for contaminated and blended transits in the BP/RP spectra. Contaminated transits are fully weighted, while blended transits are weighted at 50% (0.5) to reflect their partial impact on spectral purity:

PMCF = 1.0 - (\frac{n_{contam} + 0.5 \cdot n_{blend}}{n_{total_obs}})

Note: A low PMCF (< 0.80) indicates poor data quality, suggesting that even low Z-scores should be interpreted with caution.

Interpretation of Results

Z-Score Range	Scientific Interpretation
Z ≈ 0	Chemically consistent. High probability of a shared origin.
Z < 3	Marginally consistent within the 3σ threshold.
Z ≥ 5	Highly significant difference. Physical association is statistically excluded.

Residual Analysis

If historical measurements of the separation and position angle are provided, the Double Star Calculator performs a trend analysis on the astrometric residuals of the double star. It quantifies the deviations of the historical measurements from a kinematic motion predicted reference model based on Gaia proper motion data.

Methodology

The observational epochs are centered around a reference epoch to mitigate possible numerical instabilities of the algorithm
Raw residuals are computed for separations and position angles, while for position angles a wrap-around correction is applied
Statistics for the raw residuals are calculated: the Mean Absolute Error (MAE), the Root Mean Square Error (RMSE), and the sample standard deviation (STDEV)
Additionally, a global Durbin-Watson test is performed to detect systematic deviations from the Gaia model

The core of the residual analysis is the computation of a trend analysis (sequential polynomial fit) with three different competing regression models. For each model the Root Mean Square (RMS) is calculated and the Durbin-Watson Test are performed:

Constant Model: Estimates a purely systematic, time-invariant offset
Linear Model: Estimates a constant velocity drift discrepancy (errors in linear proper motion)
Quadratic Model: Estimates a constant acceleration component, capturing non-linear motion trends

Implementation notes

Temporal Centering

To mitigate numerical instabilities and loss of precision during higher-order polynomial fitting, the observational epochs are centered around a user-defined reference epoch (T₀ = 2000.0). For each epoch t_i, the relative epoch Δt_i is computed as:

{Δt}_{i} = t_{i} - T_{0}

Raw Residual Computation

The raw residuals are computed directly from the difference between historical measurements and the Gaia reference model. For angular separations (ρ), a linear difference is used, while Position Angles (PA) require a wrap-around correction to account for the 360° periodicity:

Angular Separation Residuals (ρ):

R_{ρ, i} = ρ_{hist, i} - ρ_{Gaia, i}

Position Angle Residuals (PA):

R_{PA, i} = ((θ_{hist, i} - θ_{Gaia, i} + 180.0) mod 360.0) - 180.0

Baseline Statistical Metrics

The global metrics for the raw residual dataset consisting of N measurements are defined as follows. The implementation in Python is based on NumPy (np):

Mean Absolute Error (MAE)

MAE = \frac{1}{N} \sum_{i = 1}^{N} | R_{i} |

PYTHON: mae = np.mean(np.abs(residuals))

Bias (Arithmetic Mean)

Bias = \frac{1}{N} \sum_{i = 1}^{N} R_{i}

PYTHON: bias = np.mean(residuals)

Root Mean Square Error (RMSE)

RMSE = \frac{1}{N} \sum_{i = 1}^{N} R_{i}^{2}

PYTHON: rmse = np.sqrt(np.mean(residuals**2))

Sample Standard Deviation (STDEV)

Calculated using Delta Degrees of Freedom (ddof = 1) to provide an unbiased estimator for smaller sample sizes:

STDEV = \frac{1}{N - 1} \sum_{i = 1}^{N} {(R_{i} - Bias)}^{2}

PYTHON: stdev = np.std(residuals, ddof=1)

Durbin-Watson Test Statistic

The Durbin-Watson score (DW) checks for sequential first-order autocorrelation between successive data records. It is computed both for the raw residuals and the post-fit residuals of the regression models using the following equation, Where ε_i represents the evaluated series (either raw residuals or post-fit residuals):

DW = \frac{\sum_{i = 2}^{N} {(ε_{i} - ε_{i - 1})}^{2}}{\sum_{i = 1}^{N} ε_{i}^{2}}

PYTHON: dw = durbin_watson(residuals)

Regression Modeling

The application fits three competing polynomial orders to the raw residuals (R_i) over the relative epochs (Δt_i). The execution uses algebraic matrix inversion via least squares minimization. For each model, the Root Mean Square (RMS) of the remaining post-fit residuals is computed.

Model 1: Constant Model

Models a systematic, static baseline shift by applying the arithmetic mean:

f_{const} ({Δt}_{i}) = a

PYTHON:
a_const   = np.mean(residuals)                          
fit_const = np.full_like(residuals, a_const)            
rms_const = np.sqrt(np.mean((residuals - fit_const)**2))
dw_const  = durbin_watson(residuals - fit_const)

Model 2: Linear Model

Models a constant velocity drift discrepancy using a standard linear slope:

f_{linear} ({Δt}_{i}) = b \cdot {Δt}_{i} + a

The coefficients b (velocity drift) and a (intercept) are obtained by minimizing the squared errors over the array. Implemented in Python as:

PYTHON:
coeff_linear = np.polyfit(t_rel, residuals, 1)              
b_lin, a_lin = coeff_linear                                 
fit_linear   = np.polyval(coeff_linear, t_rel)              
rms_linear   = np.sqrt(np.mean((residuals - fit_linear)**2))
dw_linear    = durbin_watson(residuals - fit_linear)

Model 3: Quadratic Model

Captures a constant acceleration component to trace non-linear orbital trends:

f_{quad} ({Δt}_{i}) = c \cdot {Δt}_{i}^{2} + b \cdot {Δt}_{i} + a

Where $c$ represents the acceleration coefficient. Implemented in Python as:

PYTHON:
coeff_quad             = np.polyfit(t_rel, residuals, 2)            
c_quad, b_quad, a_quad = coeff_quad                                 
fit_quad               = np.polyval(coeff_quad, t_rel)              
rms_quad               = np.sqrt(np.mean((residuals - fit_quad)**2))
dw_quad                = durbin_watson(residuals - fit_quad)

Model RMS Calculation

For each specific model fit, the remaining scatter (RMS) of the post-fit residuals is mathematically defined via:

{RMS}_{model} = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {(R_{i} - f_{model} ({Δt}_{i}))}^{2}}

Auxiliary Astrometric Functions

This chapter describes auxiliary functions used in the analysis of stellar kinematics and physical association. These functions support the main astrometric routines and provide derived quantities and comparison metrics.

Distance from Parallax

This function converts the stellar parallax into distance, expressed in parsecs and light-years, including the propagation of the parallax uncertainty.

The calculation follows the standard astronomical relation between parallax and distance and assumes Gaussian error propagation.

Distance in parsecs

d_{pc} = \frac{1000}{ϖ}

where $ϖ$ is the parallax in milliarcseconds (mas).

Uncertainty of the distance

σ_{d_{pc}} = \frac{1000}{ϖ^{2}} \cdot σ_{ϖ}

The uncertainty is derived using standard Gaussian error propagation.

Conversion to light-years

d_{ly} = d_{pc} \cdot C_{pc→ly}

σ_{d_{ly}} = σ_{d_{pc}} \cdot C_{pc→ly}

with the conversion constant $C_{pc→ly} = 3.26156$ .

Results

d_pc – distance in parsecs
σ_d,pc – distance uncertainty in parsecs
d_ly – distance in light-years
σ_d,ly – distance uncertainty in light-years

Projected Separation

Calculates a conservative lower bound of the projected physical separation in parsec between two stars by evaluating the projected separation at the average distance d_avg of both components.

s = d_{avg} \cdot \tan (θ)

Uncertainty of the projected separation

σ_{s} = d_{avg} \cdot \frac{1}{\cos^{2} (θ)} \cdot σ_{θ}

where θ is the angular separation and σ_θ the uncertainty of the angular separation.

Note: For pairs with very small angular separations (≤ 100″), the geometric projection term tan(θ) approaches zero. Consequently, the impact of the distance uncertainty (σ_d) on the physical separation error is minor and has been intentionally omitted.

Results

s – projected separation in parsec
σ_s – uncertainty of the projected separation in parsec

Absolute Magnitude

This function calculates the absolute magnitude of a star from its apparent Gaia G-band mean magnitude m_G and its distance in parsecs d_pc. This value is corrected for stellar extinction A_G (G-band) and indicated, whenever the corresponding data is available in the Gaia database.

Absolute magnitude

M_{G} = m_{G} - 5 \cdot \log_{10} (d_{pc}) + 5 - A_{G}

Uncertainty of absolute magnitude

σ_{M_{G}} = \sqrt{{(\frac{5}{\ln (10) \cdot d_{pc}} \cdot σ_{d_{pc}})}^{2} + σ_{A_{G}}^{2}}

Results

M_G – absolute magnitude
σ_{M_G} – uncertainty of absolute magnitude

Proper Motion Angular Difference

Computes the absolute angular difference between two proper motion position angles, normalized to the range 0°–180°.

Δθ = | θ_{B} - θ_{A} |

Uncertainty:

σ_{Δθ} = \sqrt{{σ_{A}}^{2} + {σ_{B}}^{2}}

Total Proper Motion Difference

Computes the absolute difference in total proper motion between two stars.

Δμ = | μ_{A} - μ_{B} |

Uncertainty:

σ_{Δμ} = \sqrt{{σ_{A}}^{2} + {σ_{B}}^{2}}

Velocity Differences

The following auxiliary functions compute absolute differences in tangential, radial, and total space velocity using identical mathematical formulations.

Generic Equation:

Δv = | v_{A} - v_{B} |

Uncertainty:

σ_{Δv} = \sqrt{{σ_{A}}^{2} + {σ_{B}}^{2}}

This formulation applies to:

Tangential velocity difference
Radial velocity difference
(Scalar) Speed difference

Relative Velocity (3D) Difference

The magnitude of the vectorial difference between the stars' 3D velocity vectors. Unlike the scalar version, this value accounts for the stars' actual directions of motion. It represents the total relative speed between the two components. The following function computes the 3D velocity difference.

Velocity Component Calculation:

v_{α, i} = k \cdot \frac{μ_{α *, i}}{ϖ_{i}}, v_{δ, i} = k \cdot \frac{μ_{δ, i}}{ϖ_{i}}

Error Propagation of Individual Components:

σ_{v_{α, i}} = \sqrt{{((\frac{k}{ϖ_{i}} σ_{μ_{α *, i}}))}^{2} + {((\frac{k \cdot μ_{α *, i}}{ϖ_{i}^{2}} σ_{ϖ_{i}}))}^{2}}

Total Velocity Difference (Δv_rel):

{Δv}_{rel} = \sqrt{{Δv}_{α}^{2} + {Δv}_{δ}^{2} + {(w_{r} \cdot {Δv}_{r})}^{2}}

Final Error Propagation (σ_Δv):

σ_{{Δv}_{rel}} = \sqrt{{(\frac{{Δv}_{α} \cdot σ_{{Δv}_{α}}}{{Δv}_{rel}})}^{2} + {(\frac{{Δv}_{δ} \cdot σ_{{Δv}_{δ}}}{{Δv}_{rel}})}^{2} + {(\frac{w_{r} \cdot {Δv}_{r} \cdot σ_{{Δv}_{r}}}{{Δv}_{rel}})}^{2}}

where $w_{r} \in {0, 1}$ .

Nomenclature & Constants

Symbol	Description	Value / Unit / Definition
$k$	au to km/s conversion factor	4.74057
$w_{r}$	Radial velocity weighting factor	1.0 (enabled) or 0.0 (disabled)
$ϖ$	Parallax	mas
$μ_{α *}$	Proper Motion in Right Ascension (μ_α · cos δ)	mas/yr
$μ_{δ}$	Proper Motion in Declination	mas/yr
$σ$	Standard uncertainty (Sigma)	Associated error of a variable
$v_{\tan}$	Tangential velocity component	km/s
$v_{r}$	Radial velocity component	km/s
${Δv}_{rel}$	Relative Velocity (3D) Difference	km/s (Vectorial Difference)

Spectral Type Estimation

Estimates the stellar spectral class and temperature using the Gaia BP–RP color index based on empirical color boundaries. The temperatures are derived from data provided by the University of Northern Iowa [8].

    Spectral class |  BP-RP  Color-Index    |  Temperature 
    ---------------|--------------------------------------
    O:             |         bp_rp < -0,1   |    50000
    B:             | -0,1  ≤ bp_rp ≤  0,3   |    15000
    A:             |  0,3  < bp_rp ≤  0,5   |     8750
    F:             |  0,5  < bp_rp ≤  0,72  |     6700
    G:             |  0,72 < bp_rp ≤  1,14  |     5800
    K:             |  1,14 < bp_rp ≤  1,8   |     4800
    M:             |         bp_rp >  1,8   |     3300
    ------------------------------------------------------

The function returns one of the spectral classes: O, B, A, F, G, K, M.

This is an approximate classification intended for statistical and comparative analysis.

Mass–Luminosity Relation

This chapter describes the estimation of stellar luminosity and mass for main-sequence stars based on their absolute magnitude and spectral type. The implemented method follows the segmented mass–luminosity relations presented by Eker et al. (2018) [9], adapted here to broad spectral-type intervals for practical application. The luminosity is derived from the absolute magnitude relative to the Sun, including a bolometric correction. The stellar mass is subsequently computed by inverting the logarithmic mass–luminosity relation.

Luminosity:

The stellar luminosity expressed in units of the solar luminosity where $M_{G}$ is the absolute Gaia G-band magnitude of the star and $M_{⊙}$ is the solar absolute bolometric magnitude, adopted here as $M_{⊙} = 4.74$ . A bolometric correction factor ( $B C$ ) according to Pecaut and Mamajek (2013), updated via the online dwarf star properties compilation (Mamajek 2022) [10] is applied based on the estimated spectral type to determine the bolometric magnitude:

    "O5V" => -3.76
    "B5V" => -1.34
    "A5V" =>  0.00
    "F5V" => -0.02
    "G5V" => -0.105
    "K5V" => -0.63
    "M5V" => -3.11

\frac{L}{L_{⊙}} = 10^{- 0.4 \cdot (M_{G} + B C - M_{⊙, bol})}

Given an uncertainty $σ_{M}$ in the absolute G-band magnitude, lower and upper luminosity limits are computed as:

L_{\min} = 10^{- 0.4 \cdot (M_{G} + σ_{M} + B C - M_{⊙, bol})}

L_{\max} = 10^{- 0.4 \cdot (M_{G} - σ_{M} + B C - M_{⊙, bol})}

Mass–Luminosity Relation and Mass Estimation:

Eker et al. (2018) describe the mass–luminosity relation for main-sequence stars as a segmented power law based on the stellar mass $ℳ$ (expressed in solar masses, $ℳ / M_{⊙}$ ):

\log_{10} (L) = α \cdot \log_{10} (ℳ) + C

Here, $α$ is the slope and $C$ the intercept of the logarithmic relation, both depending on the stellar mass regime. For mass estimation, the relation is inverted to yield:

ℳ = 10^{\frac{\log_{10} (L) - C}{α}}

Notes and Assumptions

The coefficients

α

and

C

are assigned according to broad spectral-type intervals, mapped from the segmented relations given by Eker et al. (2018). This approach provides a practical approximation for main-sequence stars when detailed stellar parameters are unavailable:

    "O" => { α: 3.96, C:  0.00 }, # High Mass
    "B" => { α: 3.96, C:  0.00 }, # High Mass
    "A" => { α: 4.67, C: -0.15 }, # Intermediate Mass
    "F" => { α: 4.67, C: -0.15 }, # Intermediate Mass
    "G" => { α: 5.56, C: -0.03 }, # Low Mass
    "K" => { α: 4.20, C: -0.20 }, # Ultra-Low Mass
    "M" => { α: 2.27, C:  0.60 }  # Ultra-Low Mass

The method is valid for main-sequence stars only.
The mass estimate is computed from the nominal luminosity value.
Luminosity limits reflect the uncertainty in absolute magnitude.
Spectral-type boundaries are approximate and intended for practical use.

Hertzsprung-Russell Diagram

The positions of both components are plotted in a simplified Hertzsprung–Russell diagram (HRD). The positions are derived from their calculated stellar luminosities, expressed in solar luminosities and converted to logarithmic scale, and from their effective temperatures (T_eff) as provided by Gaia (plotted as solid circles). The effective temperatures are taken from the Gaia GSP-Phot Aeneas solution based on BP/RP spectra (teff_gspphot) and are likewise converted to logarithmic scale. In case the effective temperature is not available, the temperature is estimated from the color index (bp_rp) measured by Gaia (plotted as open circles). Upper and lower bounds of both luminosity and effective temperature are propagated into logarithmic space to derive symmetric uncertainties for the HRD coordinates.

In addition to the stellar positions, the HRD includes schematic regions indicating the approximate locations of the main sequence, giant stars, supergiants, and white dwarfs. These regions are intended for qualitative orientation within the HR diagram and are based on standard tabulated relations between spectral type and effective temperature, such as those provided by the University of Northern Iowa [8].

Orbital Elements

The Double Star Calculator – Orbital Elements generates orbit diagrams and a corresponding ephemeris table showing the separation and position angle of a double star based on its orbital elements. This section documents the mathematical functions used to compute the apparent visual positions of a binary star system.

Mean Anomaly

The Mean Anomaly represents the time elapsed since the last periastron passage, scaled by the orbital period and expressed as an angular measure wrapped into the range 0 to 2π.

M = [\frac{2 π}{P} \cdot (t - T)] mod (2 π)

Kepler's Equation

Kepler's equation relates the eccentric anomaly E to the mean anomaly M, where the mean anomaly serves as the time-dependent parameter.e is the orbital eccentricity:

M = E - e \cdot \sin (E)

Kepler's equation is a transcendental equation and therefore cannot be solved analytically. It is solved numerically using the Newton-Raphson method. The initial guess is selected dynamically. For low-eccentricity orbits (e < 0.8), the iteration starts with E = M. For highly eccentric orbits (e ≥ 0.8), the initial guess is set to π to improve numerical convergence. The estimate of E is then iteratively refined using:

E_{n + 1} = E_{n} - \frac{E_{n} - e \cdot \sin (E_{n}) - M}{1 - e \cdot \cos (E_{n})}

The iteration terminates once the residual error falls below the specified tolerance (10^-9). A strict safety limit of 100 iterations prevents infinite loops. This is particularly important for highly eccentric binary systems (e ≈ 0.98), where convergence may become significantly slower near periastron.

True Orbital Coordinates

Once the Eccentric Anomaly is successfully resolved, the physical orbital track is evaluated using three sequential mathematical relations:

True Anomaly: Computes the actual angular position of the star in the orbital plane, measured from periastron. The calculation utilizes a quadrant-preserving arctangent (atan2) to determine the angle accurately across all four quadrants: $θ = 2 \cdot atan2 (\sqrt{1 + e} \cdot \sin (\frac{E}{2}), \sqrt{1 - e} \cdot \cos (\frac{E}{2}))$
Radius Vector: Computes the instantaneous distance between the primary star and its companion from the semi-major axis, orbital eccentricity, and Eccentric Anomaly: $r = a \cdot (1 - e \cdot \cos (E))$

Projection Onto the Sky Plane

To display the orbit as observed on the sky, the true orbital coordinates are projected onto the plane of the sky using the three Campbell elements: the position angle of the ascending node, the argument of periastron, and the orbital inclination. This transformation produces the apparent orbital ellipse:

x = r \cdot (\cos (Ω) \cdot \cos (θ + ω) - \sin (Ω) \cdot \sin (θ + ω) \cdot \cos (i))

y = r \cdot (\sin (Ω) \cdot \cos (θ + ω) + \cos (Ω) \cdot \sin (θ + ω) \cdot \cos (i))

Orbit Determination

The Double Star Calculator – Orbit Determination (DSC-OD) determines the visual orbital elements of a binary star system from a time series of relative astrometric measurements. The observational dataset consists of $N$ discrete epochs $t_{k}$ , angular separations $ρ_{k}$ (in arcseconds), and position angles $θ_{k}$ (in degrees, measured east of north):

D = {(t_{k}, ρ_{k}, θ_{k}) ∣ k = 1, \dots, N}

From these visual observations on the celestial sphere—representing the apparent projection of a true two-body Keplerian orbit—the module fits the seven classical orbital elements (the Campbell parameters):

$P$ : Orbital period (years)
$a$ : Semi-major axis of the true orbit (arcseconds)
$i$ : Inclination of the orbital plane relative to the plane of the sky (degrees)
$Ω$ : Position angle of the ascending node (degrees)
$T_{0}$ : Epoch of periastron passage (fractional year)
$e$ : Numerical eccentricity ( $0 \leq e < 1$ )
$ω$ : Argument of periastron (degrees)

Due to the non-linear relationship between the orbital elements and the apparent visual positions ( $ρ$ , $θ$ ), finding the global minimum of the objective function requires suitable initial parameter estimates. To ensure robust convergence of the non-linear solver, the algorithm provides three distinct initialisation strategies:

Simple Initial Guess Method: A heuristic estimation technique derived from data bounds, angular velocity estimates, and geometric bounding boxes.
Thiele-Innes Guess Method: A semi-analytical method utilizing geometric relationships and Thiele-Innes constants derived from selected observational points to solve for orbital orientation and scale.
Direct User Guess: Direct manual specification of initial parameters by the user, providing full control when preliminary orbital solutions are already known.

Simple Initial Guess Method

The Simple Initial Guess Estimator provides a robust starting point directly derived from the observational time domain and projected astrometric geometry for the seven orbital Campbell elements. The method is intentionally heuristic and is designed to provide stable initial values for subsequent non-linear optimization rather than physically accurate orbital elements.

Orbital Period ( $P_{0}$ )

The orbital period estimate is evaluated using the continuous, unwrapped total angular rotation $Δ θ = | θ_{unwrapped} (t_{max}) - θ_{unwrapped} (t_{min}) |$ over the observation time span $Δ t = max (t_{max} - t_{min}, 1.0)$ . If the observations cover approximately three-quarters of a full revolution or more ( $Δ θ \geq 1.5 π$ ), the time span itself serves as the period estimate; otherwise, it is conservatively scaled to twice the covered time span:

P_{0} = {\begin{matrix} Δ t & if Δ θ \geq 1.5 π \\ 2.0 \cdot Δ t & otherwise \end{matrix}

Semi-Major Axis ( $a_{0}$ )

The semi-major axis is estimated using the arithmetic mean of the maximum and minimum observed angular separations ( $ρ_{max}$ and $ρ_{min}$ ):

a_{0} = \frac{max_{k} (ρ_{k}) + min_{k} (ρ_{k})}{2}

Longitude of Ascending Node ( $Ω_{0}$ )

The longitude of the ascending node $Ω_{0}$ is aligned with the observed position angle corresponding to the epoch of maximum angular separation $ρ_{max}$ :

Ω_{0} = θ_{argmax (ρ)} mod 2 π

Argument of Periastron ( $ω_{0}$ )

The argument of periastron is initialized to zero:

ω_{0} = 0.0

Time of Periastron Passage ( $T_{0}$ )

The epoch of periastron passage is estimated by starting at the earliest observation epoch $t_{min}$ and shifting forward by 20% of the estimated orbital period $P_{0}$ :

T_{0} = t_{min} + 0.2 \cdot P_{0}

Inclination and Eccentricity ( $i_{0}$ , $e_{0}$ )

Inclination and eccentricity are assigned fixed default values. The inclination is initialized to its theoretical expectation value for isotropically oriented orbital planes in three-dimensional space ( $⟨ i ⟩ = 1.0 rad$ ):

i_{0} = 1.0 rad \approx 57.30 °, e_{0} = 0.3

Thiele-Innes Initial Guess Method

The Thiele-Innes Initial Guess Estimator simplifies orbit determination by decoupling the seven orbital parameters into two distinct sets: three non-linear orbital shape and timing parameters ( $(P, T_{0}, e)$ ), and four linear spatial orientation constants known as the Thiele-Innes constants ( $(A, B, F, G)$ ). By scanning a candidate grid over the non-linear parameter space, the optimal spatial orientation constants are determined at each node via linear least-squares. If fewer than four observations are available, or if the grid search fails to yield a physically valid solution, the algorithm automatically falls back to the Simple Initial Guess Method.

By evaluating a candidate grid of $(P, T_{0}, e)$ , the spatial orientation parameters $(A, B, F, G)$ are solved instantly via linear least-squares at each node. The parameter set yielding the lowest residual error is selected and analytically transformed into the geometric Campbell orbital elements ( $(a, i, Ω, ω)$ ).

1. Coordinate System Transformation

Observed polar astrometric coordinates (angular separation $ρ_{k}$ and position angle $θ_{k}$ ) are mapped into standard relative Cartesian coordinates on the celestial tangent plane, where $x$ represents Right Ascension offset (East) and $y$ represents Declination offset (North):

x_{k} = ρ_{k} \cdot sin (θ_{k}), y_{k} = ρ_{k} \cdot cos (θ_{k})

2. Non-Linear Parameter Space Grid Discretization

A candidate grid evaluates combinations over the bounded domain of non-linear parameters:

Orbital Period ( $P$ ): Sampled linearly over $P \in [P_{min}, P_{max}]$ , where $P_{min} = max (10.0, 0.2 Δ t)$ and $P_{max} = max (2.5 Δ t, 300.0)$ with $Δ t = t_{max} - t_{min}$ .
Eccentricity ( $e$ ): Sampled across representative values $e \in {0.1, 0.3, 0.5, 0.7}$ .
Epoch of Periastron Passage ( $T_{0}$ ): Uniformly sampled over a period window centered on the observational timeline: $T_{0} \in [t_{min} - P, t_{min} + P]$ .

3. Linear System Matrix Formulation

For each candidate grid node $(P, T_{0}, e)$ , the mean anomaly $M_{k} = \frac{2 π (t_{k} - T_{0})}{P} mod 2 π$ is converted to eccentric anomaly $E_{k}$ via Kepler's equation ( $M_{k} = E_{k} - e sin E_{k}$ ). Normalized coordinates in the true orbital plane are computed as:

X_{k} = cos (E_{k}) - e, Y_{k} = \sqrt{1 - e^{2}} \cdot sin (E_{k})

The projected positions follow the linear relations $x_{k} = A X_{k} + F Y_{k}$ and $y_{k} = B X_{k} + G Y_{k}$ . This forms an overdetermined linear system $L \cdot c = b$ :

[\begin{matrix} X_{1} & Y_{1} & 0 & 0 \\ 0 & 0 & X_{1} & Y_{1} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ X_{N} & Y_{N} & 0 & 0 \\ 0 & 0 & X_{N} & Y_{N} \end{matrix}] [\begin{matrix} A \\ F \\ B \\ G \end{matrix}] = [\begin{matrix} x_{1} \\ y_{1} \\ ⋮ \\ x_{N} \\ y_{N} \end{matrix}]

The system is solved via linear least squares:

\hat{c} = {(L^{T} L)}^{- 1} L^{T} b

The grid combination $(P, T_{0}, e, A, B, F, G)$ yielding the minimum sum of squared Cartesian residuals:

S = {‖ b - L \hat{c} ‖}_{2}^{2}

is selected as the global initial guess.

4. Analytical Transformation to Campbell Elements

The optimal Thiele-Innes constants $(A, B, F, G)$ are analytically inverted into geometric Campbell parameters ( $a, i, Ω, ω$ ). First, two fundamental algebraic invariants are evaluated:

k = A^{2} + B^{2} + F^{2} + G^{2} = a^{2} (1 + {cos}^{2} i)

m = A G - B F = a^{2} cos i

Solving the characteristic quadratic equation—including numerical safeguards against floating-point underflow—yields the semi-major axis $a$ and inclination $i$ :

a = \sqrt{\frac{k + \sqrt{k^{2} - 4 m^{2}}}{2}}, i = arccos (\frac{m}{a^{2}})

The longitude of the ascending node $Ω$ and argument of periastron $ω$ are decoupled via the van den Bos (1926) sum and difference angle equations:

θ_{1} = Ω + ω = atan2 (B - F, A + G)

θ_{2} = Ω - ω = atan2 (B + F, A - G)

Solving for $Ω$ and $ω$ yields:

Ω = \frac{θ_{1} + θ_{2}}{2} mod 2 π, ω = \frac{θ_{1} - θ_{2}}{2} mod 2 π

Orbit Fitting

The orbit determination of visual binary stars represents a non-linear inverse problem in astrometry. Given a set of N observational epochs t_k, angular separations ρ_k (in arcseconds), and position angles θ_k (in degrees, measured from North through East), the goal is to determine the seven canonical Campbell orbital elements:

P: Orbital period [years]
a: Semi-major axis of the relative orbit [arcseconds]
i: Orbital inclination [0 ≤ i ≤ π rad]
Ω: Longitude of the ascending node [0 ≤ Ω < 2π rad]
T: Epoch of periastron passage [decimal Julian years]
e: Orbital eccentricity [0 ≤ e < 1]
ω: Argument of periastron [0 ≤ ω < 2π rad]

The bounds for the calculation of the orbital elements are defined as follows:

P: (1e-3, 1e6)
a: (1e-6, 1e4)
i: (0.0, π)
Ω: (0.0, 2 * π)
T: (t_min − 2000.0, t_max + 2000.0)
e: (0.0, 0.9999)
ω: (0.0, 2 * π)

Definition and Processing of Measurement Errors

Astrometric measurements of visual binary stars originate from diverse observational techniques spanning over two centuries of historical and modern astronomy. Consequently, observational uncertainties range from subjective visual estimates to sub-milliarcsecond space-based measurements. To perform a statistically rigorous weighted orbit determination, each measurement pair, comprising angular separation ( $ρ$ ) and position angle ( $θ$ ), must be assigned individual, physically realistic 1- $σ$ standard uncertainties ( $σ_{ρ}$ and $σ_{θ}$ ).

The preprocessing pipeline parses raw observation catalogs compliant with the United States Naval Observatory (USNO) Washington Double Star (WDS) specification. It executes a deterministic multi-tier error allocation model. This model imports published formal catalog errors, applies category-specific systematic error floors in quadrature, imputes technique-dependent default values for unquantified historical data, and enforces strict defensive bounds against unphysical or zero-uncertainty values.

Catalog Import and Data Parsing Layout

Raw observation data lines adhere to the post-May/June 2012 expanded fixed-width USNO WDS observation catalog format. Data parsing is performed by extracting specific column ranges via fixed-width slicing:

Quantity	Symbol	WDS Columns	Format	Unit	Description
Observation Date	$t$	008–017	`f10.5`	Decimal Years	Epoch of observation
Position Angle	$θ$	020–026	`f7.3`	Degrees (°)	Observed position angle (0° to 360°)
PA Formal Error	$σ_{cat, θ}$	028–033	`f6.3`	Degrees (°)	Published formal uncertainty in $θ$
Separation	$ρ$	036–044	`f9.5`	Arcseconds (″)	Observed angular separation
Separation Error	$σ_{cat, ρ}$	047–053	`f7.5`	Arcseconds (″)	Published formal uncertainty in $ρ$
Technique Code	`tech`	112–113	`a2`	Text Code	Two-character observational technique identifier

Observational Technique Classification

The primary character of the two-letter technique code (column 112) maps the measurement into one of seven broad astronomical technique categories ( $C$ ). If no technique code is supplied, or an unmapped character is encountered, the record is assigned to the default fall-back category (DEF).

Category Code	WDS Technique Prefixes	Observational Methodology	Default Uncertainty ( $σ_{def, ρ}$ , $σ_{def, θ}$ )	Systematic Floor ( $σ_{sys, ρ}$ , $σ_{sys, θ}$ )
`VIS`	M, V, D, T	Visual micrometrical, meridian circle, heliometer, transit circle	0.100″, 1.000°	0.050″, 0.500°
`PHO`	P	Photographic plates / analog emulsions	0.060″, 0.600°	0.030″, 0.300°
`CCD`	C, E, A	Ground-based CCD, CMOS, electron multiplication, lucky imaging	0.035″, 0.400°	0.010″, 0.200°
`SPE`	S	Speckle interferometry	0.004″, 0.200°	0.002″, 0.100°
`INT`	I, J, K	Long-baseline optical, infrared, radio, or aperture-masking interferometry	0.002″, 0.100°	0.0005″, 0.050°
`SPA`	H	Space-based astrometry (e.g., Hipparcos, Tycho-2, Gaia, HST)	0.001″, 0.050°	0.0005″, 0.050°
`SPC`	X, Z, O	Spectroscopic binaries, eclipse minimum timing, occultation timing	0.050″, 0.500°	0.020″, 0.300°
`DEF`	Unmapped / Blank	Global fall-back for unspecified observational methods	0.100″, 1.000°	0.010″, 0.200°

Mathematical Error Model and Quadrature Addition

The assignment of final effective uncertainties ( $σ_{ρ}$ and $σ_{θ}$ ) follows a deterministic decision matrix designed to prevent over-weighting due to underestimated internal errors published in catalogs.

When a published formal error value $σ_{cat}$ is present and strictly positive ( $σ_{cat} > 0$ ), it is combined in quadrature with the corresponding category-specific systematic error floor $σ_{sys}$ :

$σ_{ρ} = \sqrt{σ_{cat, ρ}^{2} + σ_{sys, ρ}^{2}}$

$σ_{θ} = \sqrt{σ_{cat, θ}^{2} + σ_{sys, θ}^{2}}$

This quadrature addition ensures that even if an observer reports extremely small formal measurement uncertainties, the weight of the observation within the orbit fitting routine remains bounded by the physical limits of the underlying technique (e.g., atmospheric seeing limits, optical diffraction limits, or detector pixel scales).

Treatment of Missing Values, Zeroes, and Exceptional Cases

Historical catalogs frequently omit error estimates or use placeholder tokens. To ensure numerical stability and prevent mathematical singularities during matrix inversions, exception handling is governed by the following rules:

Missing Catalog Errors (Blank / Whitespace): If no numerical value is present in columns 028–033 (position angle) or 047–053 (separation), the pipeline imputes the category default uncertainty $σ_{def}$ assigned to the identified technique:
$σ_{ρ} = σ_{def, ρ} (C), σ_{θ} = σ_{def, θ} (C)$
Zero-Error Placeholders ( $σ_{cat} = 0.0$ ): In legacy catalogs, a reported error of 0.0 or 0.000 does not represent zero variance, but rather a catalog placeholder indicating unquantified precision. Evaluating ${w;}_{i} = 1 / 0^{2}$ would yield an infinite weight, forcing the orbit optimizer to pass exactly through that data point. The system intercepts all non-positive entries ( $σ_{cat} \leq 0.0$ ), rejects them as valid catalog uncertainties, and falls back to the technique category defaults $σ_{def}$ .
Malformed Numerical Format: Strings failing standard floating-point conversion (e.g., incomplete decimals starting with isolated periods or non-numeric characters) trigger an immediate parsing fallback to $σ_{def}$ .
Corrupted Core Observations: Lines containing unparseable dates ( $t$ ), missing separations ( $ρ$ ), or missing position angles ( $θ$ ) are completely rejected and omitted from the array generation phase.

Role of Effective Uncertainties in Optimization

The effective uncertainty arrays ( $σ_{ρ}$ and $σ_{θ}$ ) generated during preprocessing form the statistical foundation for the subsequent orbit determination routines. By supplying strict, non-zero standard errors for every observational pair, the pipeline enables a fully weighted $χ^{2}$ -minimization.

Ephemeris Computation and Projective Geometry

For a given epoch t_k and parameter vector p = [P, a, i, Ω, T, e, ω]^T, the theoretical position of the secondary star relative to the primary is evaluated through Kepler's laws and Campbell projection equations.

Kepler's Equation and True Anomaly

First, the mean anomaly M_k is computed from the mean motion n = 2π / P:

M_{k} = (\frac{2 π}{P} \cdot (t_{k} - T)) mod 2 π

The eccentric anomaly E_k is obtained by solving Kepler's transcendental equation:

M_{k} = E_{k} - e \cdot sin (E_{k})

The true anomaly ν_k and the orbital radius vector r_k (in the true orbital plane) are derived using standard half-angle relations:

ν_{k} = 2 \cdot arctan2 (\sqrt{1 + e} \cdot sin (\frac{E_{k}}{2}), \sqrt{1 - e} \cdot cos (\frac{E_{k}}{2}))

r_{k} = a (1 - e \cdot cos (E_{k}))

Projection onto the Plane of the Sky

The true orbit is projected onto the tangential sky plane using the argument of latitude u_k = ν_k + ω. According to standard astronomical conventions, x represents the offset toward East (Δα cos(δ)) and y represents the offset toward North (Δδ):

x_{mod, k} = r_{k} \cdot [sin (Ω) \cdot cos (u_{k}) + cos (Ω) \cdot sin (u_{k}) \cdot cos (i)]

y_{mod, k} = r_{k} \cdot [cos (Ω) \cdot cos (u_{k}) - sin (Ω) \cdot sin (u_{k}) \cdot cos (i)]

The apparent model separation ρ_mod,k and position angle θ_mod,k are extracted via:

ρ_{mod, k} = \sqrt{x_{mod, k}^{2} + y_{mod, k}^{2}}

θ_{mod, k} = arctan2 (x_{mod, k}, y_{mod, k})

Computation of the normalized cartesian residuals

The normalized cartesian residuals are computed between the observed and model-predicted relative positions of a visual binary. The observed polar measurements (separation and position angle) and their uncertainties are transformed into Cartesian East and North coordinates using rigorous error propagation. The resulting weighted residual vector is intended for least-squares optimization of the orbital elements.

Observations are mapped onto orthogonal Tangential Sky Coordinates (x_obs, y_obs):

x_{obs, k} = ρ_{obs, k} \cdot sin (θ_{obs, k}), y_{obs, k} = ρ_{obs, k} \cdot cos (θ_{obs, k})

Applying Gaussian error propagation to this coordinate transformation yields cartesian variance estimates s_x,k² and s_y,k²:

s_{x, k} = \sqrt{{sin}^{2} (θ_{obs, k}) \cdot σ_{ρ, k}^{2} + {cos}^{2} (θ_{obs, k}) \cdot {(ρ_{obs, k} \cdot σ_{θ, rad, k})}^{2}}}

s_{y, k} = \sqrt{{cos}^{2} (θ_{obs, k}) \cdot σ_{ρ, k}^{2} + {sin}^{2} (θ_{obs, k}) \cdot {(ρ_{obs, k} \cdot σ_{θ, rad k})}^{2}}}

The normalized residual vector r(p) ∈ ℝ^2N is assembled by concatenating weighted orthogonal components:

r (p) = {[\frac{x_{mod, 1} - x_{obs, 1}}{s_{x, 1}}, \dots, \frac{x_{mod, N} - x_{obs, N}}{s_{x, N}}, \frac{y_{mod, 1} - y_{obs, 1}}{s_{y, 1}}, \dots, \frac{y_{mod, N} - y_{obs, N}}{s_{y, N}}]}^{T}

Optimization Architecture

The central orbit fitting routine employs an adaptive strategy balancing global exploration and local refinement.

Local Refinement via Least Squares

Once a promising starting guess is established (via DE, Thiele-Innes grid search, or catalog values), a local Trust-Region Reflective (TRF) algorithm refines the parameters. TRF solves the bounded non-linear least-squares problem:

min_{l \leq p \leq u} S (p) = \frac{1}{2} {∥ r (p) ∥}^{2} = \frac{1}{2} \sum_{m = 1}^{2 N} r_{m}^{2} (p)

Statistical Evaluation and Uncertainty Analysis

Chi-Square and Degrees of Freedom

χ^{2} = \sum_{m = 1}^{2 N} r_{m}^{2}, dof = 2 N - 7, χ_{red}^{2} = \frac{χ^{2}}{dof}

Covariance Matrix and Parameter Standard Errors

The local curvature of the cost function is derived from the 2N × 7 Jacobian matrix J, where J_m,j = ∂r_m / ∂p_j. To handle potential rank deficiency or strong parameter correlations robustly, the covariance matrix C is evaluated via Singular Value Decomposition (SVD) pseudo-inversion:

C = {(J^{T} J)}^{+}

If unweighted fitting is performed (σ_ρ = None), the covariance matrix is scaled by χ_red². Formal 1σ standard errors for each orbital parameter p_j are given by:

σ_{p_{j}} = \sqrt{C_{j, j}}

Additionally, the condition number κ(J^TJ) = σ_max / σ_min is recorded to diagnose ill-conditioned systems.

Optimization Summary

The Optimization Summary provides quantitative measures describing the quality, robustness, and statistical consistency of the orbit determination based on the supplied observations and measurement uncertainties. It should be interpreted as a whole. Individual metrics are most meaningful when considered together, particularly in relation to the number of observations, the orbital phase coverage, and the assumed measurement uncertainties.

N observations

Number of observations used in the orbit determination. Each observation consists of a measured separation ( $ρ$ ) and position angle ( $θ$ ), contributing two residuals ( $x$ and $y$ ) to the fit.

Time span

Time interval covered by the observations, given by the minimum and maximum observation epochs. A larger time span generally improves orbit determination, especially for long-period systems, as it increases orbital phase coverage.

Orbital phase coverage

Fraction of the orbital period covered by the observations, where $P$ is the fitted orbital period. Values close to or exceeding one full period generally provide stronger constraints on the orbital elements, while smaller values indicate limited phase coverage and potential parameter degeneracies.

phase coverage = \frac{t_{max} - t_{min}}{P}

χ² (Chi-squared)

The total chi-squared value of the fit, defined as the sum of squared, uncertainty-weighted residuals, where ( $x$ , $y$ ) are the Cartesian coordinates derived from the separation and position angle, and $σ_{x}$ , $σ_{y}$ are the corresponding propagated uncertainties. χ² measures the overall disagreement between the model and the observations. In this implementation, χ² is calculated from normalized Cartesian residuals.

χ^{2} = \sum [{(\frac{x_{model} - x_{obs}}{σ_{x}})}^{2} + {(\frac{y_{model} - y_{obs}}{σ_{y}})}^{2}]

Degrees of freedom (dof)

Number of independent residuals available to evaluate the fit after accounting for the fitted model parameters. For $N$ observations and seven fitted orbital elements ( $P$ , $a$ , $i$ , $Ω$ , $T$ , $e$ , $ω$ ), the degrees of freedom are given by the equation below. A positive and sufficiently large number of degrees of freedom is required for a meaningful statistical interpretation of χ² and reduced χ².

dof = 2 \cdot N - 7

Reduced χ²

The reduced χ² indicates how well the orbital model matches the observations relative to the assumed measurement uncertainties.

χ_{red}^{2} = \frac{χ^{2}}{dof}

χ²_red ≈ 1 : Residuals are consistent with the assumed uncertainties.
χ²_red << 1 : Residuals are significantly smaller than the assumed uncertainties (potentially overestimated errors).
χ²_red >> 1 : Residuals are larger than expected, indicating a poor fit or underestimated uncertainties.

Optimization status

Indicates whether the numerical optimization converged (Converged or Not converged).

Covariance condition number

The condition number ( $κ$ ) of the covariance matrix. Quantifies the numerical stability of the inversion and parameter correlations during the fit. It serves as a scalar measure for the numerical stability of the linear inversion and the degree of parameter correlation.

Excellent (< 10⁵): : Negligible parameter correlation; orbital elements are well constrained.
Good (10⁵ – < 10⁸): : Minor parameter correlation; typical for orbits with good phase coverage.
Fair (10⁸ – < 10¹²): : Moderate to strong parameter coupling (e.g., period P vs. semi-major axis a); parameter errors are interdependent.
Poor (10¹² – < 10¹⁶): : Strong parameter degeneracy; standard uncertainties (σ) are numerically and statistically unreliable
Very Poor (≥ 10¹⁶): : Ill-Conditioned, near-singular matrix; severe parameter degeneracy (e.g., straight-line arc, i ≈ 0°, or e ≈ 0)
Unknown: : Covariance matrix could not be inverted

RMS separation

Root-mean-square (RMS) residual of the separation (ρ), calculated from the differences between observed and modeled separations. This value quantifies the typical deviation of the observations from the model.

RMS (ρ) = \sqrt{\frac{1}{N} \cdot \sum {(ρ_{model} - ρ_{obs})}^{2}}

Weighted RMS (WRMS) Residuals

While standard RMS residuals treat all observation epochs equally, the Weighted Root Mean Square (WRMS) residuals account for varying measurement uncertainties. Each residual is weighted by the inverse square of its individual observational error (σ), ensuring that high-precision measurements (e.g., modern interferometry or space-based astrometry) have a stronger influence on the overall quality assessment than historical visual observations with higher uncertainties.

The weighting factor $w_{i}$ for an observation epoch i is calculated as:

$w_{i} = \frac{1}{{σ_{i}}^{2}}$

The WRMS residuals for the separation ( ${WRMS}_{ρ}$ ) and position angle ( ${WRMS}_{θ}$ ) are defined as:

Weighted RMS Separation (arcsec):

{WRMS}_{ρ} = \sqrt{\frac{\sum_{i = 1}^{N} w_{ρ, i} \cdot r_{ρ, i}^{2}}{\sum_{i = 1}^{N} w_{ρ, i}}}

Weighted RMS Position Angle (deg):

{WRMS}_{θ} = \sqrt{\frac{\sum_{i = 1}^{N} w_{θ, i} \cdot r_{θ, i}^{2}}{\sum_{i = 1}^{N} w_{θ, i}}}

Where $r_{ρ, i} = ρ_{obs} - ρ_{calc}$ and $r_{θ, i} = θ_{obs} - θ_{calc}$ represent the individual O−C residuals at epoch i. If individual observational errors are omitted, the calculation falls back to standard unweighted RMS statistics.

RMS position angle

Root-mean-square (RMS) residual of the position angle ( $θ$ ), calculated from the differences between observed and modeled angles. The RMS position angle reflects the typical angular discrepancy between the model and the observations.

Note: Angular differences ( $θ_{model} - θ_{obs}$ ) are phase-wrapped to the range [−180°, 180°] prior to squaring to handle the 360° boundary discontinuity correctly.

RMS (θ) = \sqrt{\frac{1}{N} \cdot \sum {[{(θ_{model} - θ_{obs})}_{wrapped}]}^{2}}

RMS spatial PA arc ( $ρ \cdot \sin Δ θ$ )

The root-mean-square (RMS) of position angle residuals projected into spatial arc length by multiplying the angular offset $Δ θ$ (in radians) by the observed separation $ρ$ .

Max separation residual

Maximum absolute residual of the separation ( $ρ$ ). This value highlights the largest individual deviation between an observed separation and the corresponding model prediction.

max | ρ_{model} - ρ_{obs} |

Max PA residual

Maximum absolute residual of the position angle ( $θ$ ), dynamically wrapped to ensure correct boundary evaluation. This value highlights the largest individual angular deviation.

max | {(θ_{model} - θ_{obs})}_{wrapped} |

Estimated 1- $σ$ Parameter Uncertainties

This subsection lists the formal 1- $σ$ standard uncertainties for the 7 fitted orbital elements. When a valid $7 \times 7$ covariance matrix $cov$ is available, uncertainties are evaluated from the diagonal elements:

$σ_{i} = \sqrt{{cov}_{i, i}}$

If a diagonal element is non-positive ( ${cov}_{i, i} \leq 0$ ) or the covariance matrix cannot be computed, the uncertainty for that parameter is set to NaN. Angular uncertainties ( $i$ , $Ω$ , $ω$ ) are automatically converted from radians to degrees.

Key	Parameter	Symbol	Description	Units
`P`	Period	$P$	Orbital period	yr
`a`	Semi-major axis	$a$	Semi-major axis	arcsec
`i`	Inclination	$i$	Inclination angle	degrees
`Omega`	Node	$Ω$	Longitude of the ascending node	degrees
`T`	Periastron passage	$T$	Epoch of periastron passage	yr
`e`	Eccentricity	$e$	Orbital eccentricity	--
`omega`	Arg. of periastron	$ω$	Argument of periastron	degrees

Note: For highly non-linear fitting problems or large condition numbers, these asymptotic 1- $σ$ errors represent a lower bound on the true uncertainties (Cramér-Rao bound).

Estimated Orbit Grade

To provide an automated and objective assessment of the calculated orbital elements, the software computes an Estimated Orbit Grade on a numerical scale from 1 (Definitive) to 5 (Indeterminate). This classification scheme is conceptually aligned with the grading system used in the USNO Sixth Catalog of Orbits of Visual Binary Stars, combining observational completeness, parameter stability, and numerical quality into a single metric.

Methodology and Evaluated Parameters

The grading algorithm evaluates the fit results in a hierarchical decision tree based on five primary key performance indicators:

Orbital Phase Coverage ( $Δ t / P$ ): The ratio of the total observation time span ( $Δ t = T_{max} - T_{min}$ ) to the fitted orbital period (P).
Periastron Passage Coverage (T in bounds): A boolean check evaluating whether the time of periastron passage (T) falls directly within the observed date range ( $T_{min} \leq T \leq T_{max}$ ). Capturing the high-velocity periastron arc significantly stabilizes the fit even when total phase coverage is low.
Relative Period Uncertainty ( $σ_{P} / P$ ): The 1-σ standard error of the orbital period divided by the period itself, serving as a direct measure of orbital scale stability.
Covariance Condition Number (K): The condition number of the covariance matrix, indicating mathematical stability and parameter decoupling.
Number of Observations (N_obs): The total count of astrometric measurement epochs included in the optimization.

Decision Logic and Grade Criteria

Grades are assigned sequentially from Grade 1 down to Grade 5. The first set of conditions that is fully satisfied determines the final grade. Unless explicitly stated otherwise (e.g., using an explicit OR or ANY operator), all conditions listed for a particular grade must be satisfied simultaneously (logical AND).

Grade	Rating Label	Evaluation Criteria / Decision Rules	Description
1	Definitive	Phase coverage $Δ t / P \geq 0.90$ (90%) Relative period error $σ_{P} / P < 0.05$ (5%) Number of observations $N_{obs} \geq 30$ Condition number $K < 10^{7}$ Weighted RMS separation ${WRMS}_{ρ} \leq 0.15 ″$	Full or near-full orbital coverage; extremely well-constrained parameters and low residuals.
2	Good	Phase coverage $Δ t / P \geq 0.55$ OR ( $Δ t / P \geq 0.35$ with Periastron observed) Relative period error $σ_{P} / P < 0.15$ (15%) Number of observations $N_{obs} \geq 20$ Weighted RMS separation ${WRMS}_{ρ} \leq 0.30 ″$	Well-observed arc with reliable parameters, well-managed residuals, and high confidence.
3	Reliable	Phase coverage $Δ t / P \geq 0.30$ OR ( $Δ t / P \geq 0.20$ with Periastron observed) Relative period error $σ_{P} / P < 0.30$ (30%) Number of observations $N_{obs} \geq 10$	Partial orbit coverage; key features or periastron passage captured.
4	Preliminary	Phase coverage $Δ t / P \geq 0.10$ (10%) Relative period error $σ_{P} / P \leq 0.60$ (60%)	Short observational arc; period and major semi-axis remain subject to revision.
5	Indeterminate	Triggered if ANY of the following apply: Condition number $K \geq 10^{16}$ (ill-conditioned matrix) Phase coverage $Δ t / P < 0.10$ Relative period error $σ_{P} / P > 0.60$ Weighted RMS separation ${WRMS}_{ρ} > 1.00 ″$ Optimization failure, invalid P, or uninvertible covariance matrix	Extremely short arc, severe parameter degeneracy, excessive observational scatter, or numerical instability.

Diagnostic Notes

Automated health flags and diagnostic messages evaluated during orbit optimization to highlight numerical instabilities, data coverage limitations, or statistical anomalies:

Degrees of Freedom ( $dof \leq 0$ ): Triggered when the number of observational constraints is insufficient relative to the fitted parameters, preventing statistical evaluation of the fit.
Goodness-of-Fit Alerts ( $χ_{red}^{2}$ ):
- $χ_{red}^{2} < 0.5$ : Residuals are significantly smaller than assumed measurement uncertainties, indicating that observational errors may be overestimated.
- $χ_{red}^{2} > 5.0$ : Indicates poor fit quality or underestimated measurement uncertainties.
Low Sample Size ( $N_{obs} < 10$ ): Warns that the orbit is weakly constrained due to fewer than 10 observations.
Eccentricity Extreme Flags:
- Nearly Circular ( $e < 0.001$ ): The argument of periastron ( $ω$ ) becomes ill-defined.
- High Eccentricity ( $e > 0.95$ ): The orbit fit depends very strongly on observations around the periastron passage.
Limited Phase Coverage:
- Very Limited Coverage ( $< 1 %$ of Period): Observations span less than 1% of the period, making $P$ poorly determined.
- Limited Coverage ( $< 30 %$ of Period): Observations span less than 30% of the orbital period, leaving the orbit weakly constrained.
High Covariance Condition Number:
- $κ > 10^{12}$ : Strong parameter correlations; uncertainty estimates may be unreliable.
- $κ > 10^{14}$ : Severe parameter degeneracy; orbit solution is poorly constrained and parameter uncertainties are unreliable.
Uncertainty Determination Failure: Flagged when one or more parameter uncertainties could not be reliably determined from the covariance matrix (resulting in NaN values).
Optimization Convergence Failure: Appears when the numerical optimization routine fails to converge, displaying the specific solver message (opt_message).

History

Version 1.0 : https://doi.org/10.5281/zenodo.19160070

Version 1.1 : https://doi.org/10.5281/zenodo.19474677

Version 1.2 : https://doi.org/10.5281/zenodo.22309756

Disclaimer

The algorithms used in the Double Star Calculator were developed and implemented by me to the best of my knowledge and belief. I have thoroughly tested the tool, and it provides plausible results based on GAIA data. However, I do not warrant the accuracy, completeness, or correctness of the results. This tool is provided "as is" without any guarantees regarding its suitability for a specific purpose or non-infringement of third-party rights.

The use of this tool is entirely at your own risk. I assume no liability for any damages, including but not limited to direct, indirect, incidental, or consequential damages, arising from the use of this tool or any errors or inaccuracies in the results.

This tool is intended for informational and research purposes only and is not a substitute for professional scientific or astronomical analysis. I reserve the right to modify, update, or discontinue the tool at any time without prior notice.

If the Double Star Calculator has been helpful in your work, a citation or acknowledgment would be greatly appreciated.

Privacy Notice: This tool does not collect, store, or process any personal data from users.

Copyright (C) 2026. The documentation is licensed under CC BY 4.0. Unless otherwise noted, all output generated by the Double Star Calculator including orbit diagrams, ephemerides, and analytical reports is licensed under CC BY 4.0.

Acknowledgements

The Double Star Calculator makes use of data from the European Space Agency (ESA) mission Gaia, processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Additionally, it incorporates data from the Washington Double Star Catalog, maintained at the U.S. Naval Observatory, makes use of the Aladin Sky Atlas developed at CDS, Strasbourg Observatory, France, and makes use of the SIMBAD database, operated at CDS, Strasbourg, France.

References

[1] Wichmann, H. (2026), Double Star Calculator, https://www.stella-vega.de/ds/

[2] Wichmann, H. (2026), Double Star Calculator - Technical Documentation, https://stella-vega.de/ds/ds_documentation.html

[3] Harshaw, Richard W. (2016), CCD Measurements of 141 Proper Motion Stars: The Autumn 2015 Observing Program at the Brilliant Sky Observatory, Part 3 (Journal of Double Star Observations, Vol. 12 No. 4 April 22, page 394), http://www.jdso.org/volume12/number4/Harshaw_394_399.pdf

[4] Tian, Hai-Jun; El-Badry, Kareem; Rix, Hans-Walter; Gould, Andrew (2020), The Separation Distribution of Ultrawide Binaries across Galactic Populations (The Astrophysical Journal Supplement Series, 246:4), https://ui.adsabs.harvard.edu/abs/2020ApJS..246....4T/abstract

[5] El-Badry, Kareem; Rix, Hans-Walter; Heintz, Tyler M. (2021), A million binaries from Gaia eDR3: sample selection and validation of Gaia parallax uncertainties (Monthly Notices of the Royal Astronomical Society, Volume 506, Issue 2, Pages 2269–2295), https://ui.adsabs.harvard.edu/abs/2021MNRAS.506.2269E/abstract

[6] J. A. Correa-Otto and R. A. Gil-Hutton (2017), Galactic perturbations on the population of wide binary stars with exoplanets (A&A, Volume 608, December 2017), https://www.aanda.org/articles/aa/abs/2017/12/aa31229-17/aa31229-17.html

[7] R. Andrae, M. Fouesneau, R. Sordo, et al. (2023), Gaia Data Release 3, Analysis of the Gaia BP/RP spectra using the General Stellar Parameterizer from Photometry (A&A, Volume 674, June 2023), https://www.aanda.org/articles/aa/full_html/2023/06/aa43462-22/aa43462-22.html

[8] University of Northern Iowa, Spectral type characteristics, https://sites.uni.edu/morgans/astro/course/Notes/section2/spectraltemps.html

[9] Eker, Z.; Bakış, V.; Bilir, S.; et al. (2018), Interrelated main-sequence mass–luminosity, mass–radius, and mass–effective temperature relations, (Monthly Notices of the Royal Astronomical Society, Volume 479, Issue 4, Pages 5491–5511), https://ui.adsabs.harvard.edu/abs/2018MNRAS.479.5491E/abstract

[10] Pecaut, M. J.; Mamajek, E. E. (2013), Intrinsic Colors, Temperatures, and Bolometric Corrections of Pre-main-sequence Stars, (The Astrophysical Journal Supplement, Volume 208, Issue 1, article id. 9), https://ui.adsabs.harvard.edu/abs/2013ApJS..208....9P/abstract, updated via the online compilation: Mamajek, E. E., 2022, A Modern Mean Dwarf Stellar Color and Effective Temperature Sequence, Version 2022.04.16, https://www.pas.rochester.edu/~emamajek/EEM_dwarf_UBVIJHK_colors_Teff.txt

[11] Roderick R. Letchford, Graeme L. White, Carolyn J. Brown (2022), Orbital Elements of visual binary stars with very short arcs: With application to double stars from the 1829 southern double star catalog of James Dunlop, (Astronomical Notes, Volume 343, Issue3), https://onlinelibrary.wiley.com/doi/10.1002/asna.20210113

☰Double Star Calculator - Technical Documentation

Abstract

Core Astrometric and Kinematic Functions

Angular Separation

Arguments

Results

Angular Separation

Error Propagation

Position Angle

Arguments

Results

Position Angle

Error Propagation

Separation and position angle as a function of Epoch

Right Ascension for target epoch

Declination for target epoch

Error Propagation

Parameters

Spatial Separation

Arguments

Results

Spatial separation

Error propagation

Parallax Significance Indicator

3D Space Velocity Vector Angle Analysis

3D Space Velocity Vector Construction

Numerically Stable 3D Vector Angle

Uncertainty Propagation via Numerical Finite Differences

Proper Motion and Velocity Analysis

Proper Motion Vector Angle

Uncertainty of the Proper Motion Angle

Total Proper Motion

Uncertainty of Total Proper Motion

Tangential Velocity

Uncertainty of Tangential Velocity

Space Velocity

Uncertainty of Space Velocity

Results

Kinematic and Dynamical Linkage Analysis

Harshaw 2D Methodology (rPM)

Harshaw Classification Levels

Uncertainty-Weighted Likelihood Estimator

Velocity Evidence Indicator

Distance Evidence Indicator

Total Evidence Indicator

Evidence Indicators - Summary

3D Spatial Distance Probability Analysis

Physical Boundary Condition & Truncation Motivation

Cumulative Probability

Dynamic & Astrophysical Threshold Evaluation

Critical Binding Distance according to Letchford et al. (2022)

Integration into the Probability Framework

Orbital & Binding Dynamics

Derivation of the Binding Indicator (η)

Metallicity Analysis [M/H]

Residual Analysis

Methodology

Implementation notes

Temporal Centering

Raw Residual Computation

Baseline Statistical Metrics

Durbin-Watson Test Statistic

Regression Modeling

Model RMS Calculation

Auxiliary Astrometric Functions

Distance from Parallax

Distance in parsecs

Uncertainty of the distance

Conversion to light-years

Results

Projected Separation

Uncertainty of the projected separation

Results

Absolute Magnitude

Absolute magnitude

Uncertainty of absolute magnitude

Results

Proper Motion Angular Difference

Total Proper Motion Difference

Velocity Differences

Orbital Period ( $P_{0}$ )

Semi-Major Axis ( $a_{0}$ )

Longitude of Ascending Node ( $Ω_{0}$ )

Argument of Periastron ( $ω_{0}$ )

Time of Periastron Passage ( $T_{0}$ )

Inclination and Eccentricity ( $i_{0}$ , $e_{0}$ )

RMS spatial PA arc ( $ρ \cdot \sin Δ θ$ )

Estimated 1- $σ$ Parameter Uncertainties